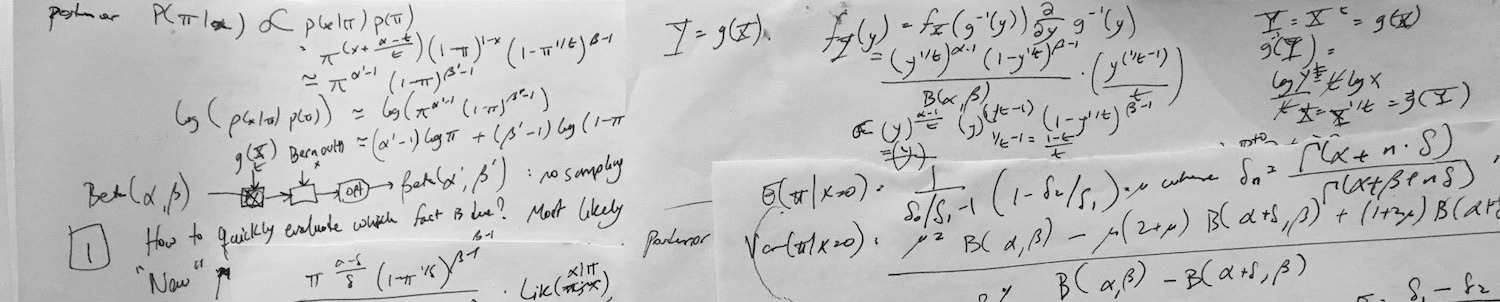
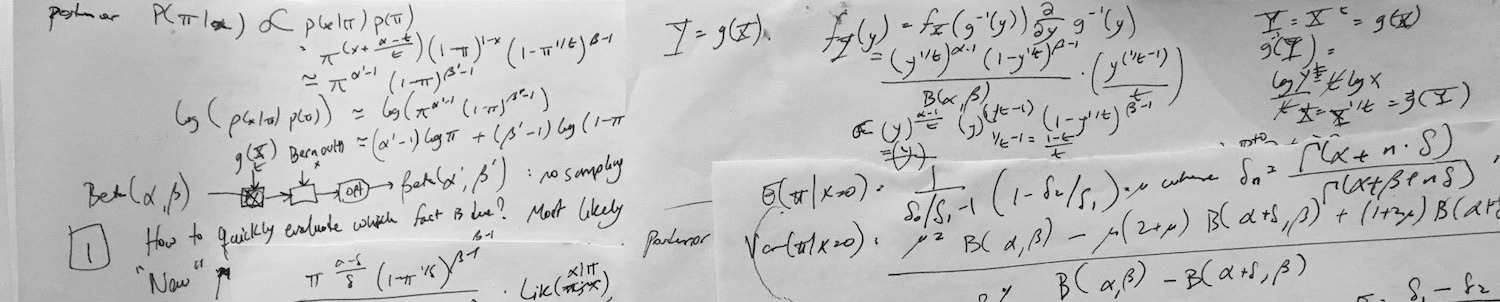
Updated on Fri, 28 Apr 2017 08:48:19 GMT, tagged with ‘tech’.
I am very pleased to announce the release of Ebisu and Ebisu.js!
These are are public-domain software libraries intended to be used by quiz or flashcard apps for intelligent, Bayesian quiz scheduling. They are released under the completely free Unlicense, and can be used anywhere by anyone without any conditions 🎆. The underlying algorithm is based on a principled application of Bayesian statistics, and has many nice features compared to existing scheduling algorithms 😁.
Ebisu is the reference Python implementation (available on PyPI) that is accompanied by detailed mathematical exposition, cool plots, and unit tests that check the math against alternative implementations.
Ebisu.js is the JavaScript port (available on npm). This link has fewer details but does include a couple of interactive visual demos to help understand what the algorithm is doing under the hood—though this understanding is purely educational.
Quiz app authors can use either library, or port the algorithm to another language, and use it as a black box module for handling quiz scheduling. You don’t need a deep understanding of Bayesian statistics or the underlying statistics, but, if you are curious 🤓: the scheduling algorithm places a probability distribution on the recall probability at one specific time, and propagates this distribution through time. In this way, it can (1) predict at any given time the recall probability for any fact that a student has already learned. The algorithm can then (2) update its belief about the recall probability when the student passes or fails a quiz.
This all means you’re not limited to any minimum interval, like one day in Anki—the algorithm might predict a 95% recall probability for one fact, 90% for a second, and 26% for the third, so of course the quiz app should test the student on the third fact. Then, if the student wants to continue reviewing, they can be tested on the second fact—with 90% recall probability—Ebisu can provide on-demand estimates of recall probability for any learned fact, and gracefully handles over-reviewing.
It also handles under-reviewing just fine: there’s no concept of “due date” in Ebisu, just recall probabilities, which are ordinary numbers between 0 (sure to fail) and 1 (sure to pass). If a student skips studying for a few days, each fact still gets a recall probability, which you can sort and review those facts most in danger of being forgotten.
As an extra bonus, Ebisu also elegantly handles “passive reviews”, i.e., those situations where the student is just shown a fact without actively having to provide an answer, and there is no “pass” or “fail”. This is nice because many students sometimes enjoy passive review, and because passive reviews frequently pop up when reviewing a fact made up of multiple sub-facts (like fill-in-the-blank with all blanks but one filled in).
This was a really cool library to design and develop, for a few different reasons.
§1. It filled several pages with probability priors and posteriors, random variable transforms, integrals, and algebraic simplification. I’ll admit: even though I was helped a lot by Wolfram Alpha, and triple-checked the results using different numerical techniques, I was surprised at still being able to do this level of math.
§2. Also—though the Ebisu algorithm turned out to be very rigorous and principled, with no corners cut, I didn’t really have a good idea what I was looking for when I started playing with the basic idea, of exponentially-decaying half-lives, from Duolingo’s half-life regression (see the link for a link to their technical conference paper). Here, “half-life” means the time it takes for the recall probability of a fact you just reviewed to drop by 50%, which Duolingo’s approach estimates for each fact and each user. Indeed, my question on the Statistics StackExchange and the PyMC code in the earliest Ebisu commits reveal how ill-formed the concept was: I was thinking about putting a probability distribution on the half-life like Duolingo did, and planning to get the time-depdendant distribution of the recall probability from there (I was really worried about how I’d make Monte Carlo sampling efficient on mobile, etc).
The key breakthrough, which is only of historic interest and doesn’t at all arise in the mathematical description of the final algorithm, was realizing that I could completely dispense with modeling the half-life itself. This was a slow surprise that took its time to dawn in my weak brain. It might be helpful to some to note how this process happened. I was sketching the following pseudocode:
recall probability = 2^(-1 * time elapsed since last review / half-life),and I noticed that I didn’t need to make the round-trip, from samples from the recall probability posterior (step 4) to half-life posterior (step 5) back to the recall probability prior (step 2). I could reuse samples from step 4 directly to get samples for step 2 for the next round. That’s what I mean when I said above that we can “completely dispense with modeling the half-life itself”, and just work with Beta priors on recall probability.
This was the key breakthrough but it still left me with Monte Carlo sampling for predicting and updating recall probabilities. I shudder to think what would have happened if I hadn’t casually gone to Wolfram Alpha to see if I could get an analytic expression for, of all the silly things, the median (or possibly mode) of the predicted recall probability right now. Recall, I had Beta samples representing the recall probability after some specific amount of elapsed time since review, and I exponentiated these to represent the recall probability right now. At that point, a sample mean was a perfectly acceptable way to collapse these samples into a scalar estimate of recall probability right now. I thought it would be fancy to get this median/mode analytically, so I manually performed the random variable transform to get the analytic distribution of the exponentiated-Beta distribution, simplified it with Wolfram Alpha, and was surprised when both the median and mode (peak density) of the resulting distribution was analytically tractable.
The mode was a dirt-simple expression and even the median was a tractable function involving evaluation of the hypergeometric function (no idea what that is, but Scipy had hyp2f1 so I was fine).
Huh. So I committed those two results and then must have started wondering what else I could do analytically—because I was really unhappy with the idea of doing quiz scheduling using Monte Carlo sampling, thousands of samples, etc., but didn’t really dare to hope for something simpler. After a lot of Wolfram Alpha-based derivations and manual simplifications (a lot of manual simplification, on pen-and-paper, even with Wolfram Alpha), it dawned on me that I needed to do absolutely no Monte Carlo sampling—every single value I needed to predict and update recall probabilities was analytically tractable, and moreover, just needed the log-gamma special function.
This fills me with joy.
From the hard-won realization that I could operate solely on recall probability and totally ignore half-life, and then the serendipitous discovery of a scary integral’s analytical solution, leading to the most surprising discovery of all, that all the scary integrals were analytically tractable—I was surprised it all worked out so nicely and can be expressed so compactly in both math and in code: Ebisu.js implements the core five-ish equations in about fifty lines of code, with Stdlib.js-provided gammln.
§3. A third reason this library was so cool to write (yes, we just finished only the second) was that it led me to Stdlib.js, a project that surprised me so much that I backed its founder on Patreon (with a very modest sum, unfortunately). It contains rigorous JavaScript implementations of all sorts of core math routines (sampling from a Beta distribution ✅; log-gamma function evaluation, ✅!), tested against best-of-class implementations from Julia, R, and Python, and with a more disciplined contributor workflow than I’ve seen on any project at Real Work.
§4. A fourth reason I enjoyed this library is because I can finally say that I made a literate Markdown document—literate as in, literate program. That is, I worked on the Ebisu Python library entirely in a single Markdown file (README.md) in Atom, evaluating code blocks by sending them to a Jupyter Python kernel via the Hydrogen plugin—which a few months ago got the ability to handle multi-programming-language Markdown files, with each code block going to the correct Jupyter kernel automatically, go Hydrogen! After ensuring that everything was working correctly, including unit tests and plots and everything, I added a special comment to the top of a few code blocks that indicated what file they should be written to, and write a small JavaScript script to “tangle” (in Knuth’s literate programming jargon) the Markdown file into actual source files. Finally, I ironed out how to use Pandoc and MathJax to convert the Markdown into web-ready HTML including math (I need to do this till the end because Atom has Markdown preview!).
It was very satisfying to finally be able to say, after a number of smaller projects using Hydrogen and Markdown, that I’d written a literate document, with the prose/math exposition sitting alongside the code, and very frequently guiding the code, and that document being tangled into a proper Python library (up on PyPI and all!—another first for me!) and weaved into a complete HTML document.
Of all these aspects of the literate program, the best was how often writing the prose explanation forced me to refactor or reorganize the code: I’d say there were about ten times where I noticed sloppy code that worked but was bad because of how awkward it was to explain in prose, and that awkwardness forcing me to improve the code so the prose would flow better. Inline documentation has a little bit of this effect but when the source is sitting right next to the prose, both brilliantly highlighted in Atom (rather than commented docs being dark gray on lighter gray!), it was easy to find the motivation to make even major improvements to how the code worked and what it looked like. (And as usual, having unit tests to protect me from incorrect changes was a huge help.)
This blog post hopefully gives some insight into how the library came about, and spoke to the craft of coding as well as the artifact that resulted. I am very excited to work on a flashcard app that uses Ebisu—there are likely more surprises in store as we experiment and gain experience with it, so the story is not over!
Previous: Announcing: KanjiBreak
Next: Co-housing